Compressão Digital de Audio
AUDIO DIGITAL - Publicado na M&T em duas partes- nº s 110 e 111
Novembro/Dezembro/2007
Por Vinicius Brazil
I – Introdução
Nas duas últimas décadas a febre das pesquisas em torno da compressão de dados foi realmente impressionante. Os pesquisadores das áreas de Dados, Vídeo e Áudio se uniram na busca da redução da relação mídia/volume de dados devido a enorme e crescente necessidade dos meios de armazenamento e também em virtude das limitações impostas pelos canais de dados a nível de sistema e de transmissão. Em face a crescente taxa de dados devido ao aumento da complexidade dos aplicativos, e, com o advento da digitalização da área de Broadcast fez-se necessário a implementação de novas técnicas de processamento digital para poder “acomodar” o enorme fluxo de dados aos meios de transmissão então disponíveis. Paralelamente, a sofisticação tecnológica atingiu em cheio a Internet, permitindo aplicativos de áudio e vídeo em tempo real que seriam impossíveis sem estas mesmas técnicas de compressão.
II - Técnicas de Compressão
Atualmente existem uma infinidade de técnicas e algoritmos que implementam a redução de bit rate do áudio e a cada Convenção da AES (Áudio Engineering Society) novas filosofias são apresentadas . Conceituou-se duas filosofias de compressão, aquelas com perdas e as sem perdas. Entretanto, este conceito não é tão óbvio e, dependendo de diversas condições, uma técnica convencionada como Lossy (com perdas) pode não possuir perdas, como veremos mais a frente. Atualmente existem uma infinidade de técnicas e algoritmos no mercado, mas, na grande maioria dos casos, são combinações de algumas das filosofias abaixo, as quais comentaremos:
II.1 - Non-Uniform PCM Coding
II.2 - Differential Coding (DPCM)
II.3 - Adaptive Differential Coding (ADPCM)
II.4 - Floating Point Coding & Floating Point Block Coding
II.5 - Masking
II.6 - Linear & Adaptive Predictive Coding
II.7 - Sub Band Coding
II.8 - Transform Coding (Spectral Coding)
II.9 – Lossless Coding
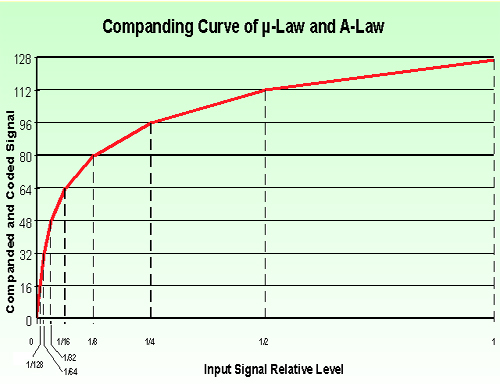
II.1 - Non-Uniform PCM Coding
Esta forma de codificação faz uso de uma função de transferência não linear. É uma das mais antigas técnicas de compressão em uso, principalmente em meios telefônicos, utilizada originalmente na forma analógica (Conpander analógico).
Exemplos:
* A-Law (Voice Transmission - USA & Japão - bit reduction rate = 14:8)
* m-Law (Idem - Europa)
* Video-8 (BRR= 10:8)
Vantagens:
* Relação 1:1 mantida para baixos sinais e Signal-Quantization NR constante para todas as bandas (>39dB no caso de BRR 14:8)
Novembro/Dezembro/2007
Por Vinicius Brazil
I – Introdução
Nas duas últimas décadas a febre das pesquisas em torno da compressão de dados foi realmente impressionante. Os pesquisadores das áreas de Dados, Vídeo e Áudio se uniram na busca da redução da relação mídia/volume de dados devido a enorme e crescente necessidade dos meios de armazenamento e também em virtude das limitações impostas pelos canais de dados a nível de sistema e de transmissão. Em face a crescente taxa de dados devido ao aumento da complexidade dos aplicativos, e, com o advento da digitalização da área de Broadcast fez-se necessário a implementação de novas técnicas de processamento digital para poder “acomodar” o enorme fluxo de dados aos meios de transmissão então disponíveis. Paralelamente, a sofisticação tecnológica atingiu em cheio a Internet, permitindo aplicativos de áudio e vídeo em tempo real que seriam impossíveis sem estas mesmas técnicas de compressão.
II - Técnicas de Compressão
Atualmente existem uma infinidade de técnicas e algoritmos que implementam a redução de bit rate do áudio e a cada Convenção da AES (Áudio Engineering Society) novas filosofias são apresentadas . Conceituou-se duas filosofias de compressão, aquelas com perdas e as sem perdas. Entretanto, este conceito não é tão óbvio e, dependendo de diversas condições, uma técnica convencionada como Lossy (com perdas) pode não possuir perdas, como veremos mais a frente. Atualmente existem uma infinidade de técnicas e algoritmos no mercado, mas, na grande maioria dos casos, são combinações de algumas das filosofias abaixo, as quais comentaremos:
II.1 - Non-Uniform PCM Coding
II.2 - Differential Coding (DPCM)
II.3 - Adaptive Differential Coding (ADPCM)
II.4 - Floating Point Coding & Floating Point Block Coding
II.5 - Masking
II.6 - Linear & Adaptive Predictive Coding
II.7 - Sub Band Coding
II.8 - Transform Coding (Spectral Coding)
II.9 – Lossless Coding
II.1 - Non-Uniform PCM Coding
Esta forma de codificação faz uso de uma função de transferência não linear. É uma das mais antigas técnicas de compressão em uso, principalmente em meios telefônicos, utilizada originalmente na forma analógica (Conpander analógico).
Exemplos:
* A-Law (Voice Transmission - USA & Japão - bit reduction rate = 14:8)
* m-Law (Idem - Europa)
* Video-8 (BRR= 10:8)
Vantagens:
* Relação 1:1 mantida para baixos sinais e Signal-Quantization NR constante para todas as bandas (>39dB no caso de BRR 14:8)
II.2 - Differential Coding
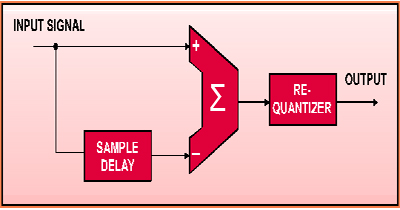
Esta técnica codifica apenas a diferença entre as amostras, levando em conta que o áudio apresenta uma correlação significativa entre amostras sucessivas, ou seja, no áudio, a diferença entre amostras consecutivas é normalmente bem menor que as mesmas. A diferença entre amostras consecutivas é codificada linearmente.
Esta técnica é considerada com perdas quando ocorrem diferenças maiores que a largura da palavra de codificação. Esta largura caracterizará a taxa de compressão do processo. Se um dado sinal de áudio é de 16 bits stereo @ 44.1kHz e codificamos as diferenças com 6 bits, a taxa de compressão será de aproximadamente 2,67 (16/6) e este material comprimido seria transmitido em um canal serial a uma taxa mínima de 529.2 kbits/s. Dependendo do material a ser comprimido e desta taxa, o processo pode ser sem perdas.
Exemplo: Dolby ADM (Adaptive Delta Modulation)
Esta técnica codifica apenas a diferença entre as amostras, levando em conta que o áudio apresenta uma correlação significativa entre amostras sucessivas, ou seja, no áudio, a diferença entre amostras consecutivas é normalmente bem menor que as mesmas. A diferença entre amostras consecutivas é codificada linearmente.
Esta técnica é considerada com perdas quando ocorrem diferenças maiores que a largura da palavra de codificação. Esta largura caracterizará a taxa de compressão do processo. Se um dado sinal de áudio é de 16 bits stereo @ 44.1kHz e codificamos as diferenças com 6 bits, a taxa de compressão será de aproximadamente 2,67 (16/6) e este material comprimido seria transmitido em um canal serial a uma taxa mínima de 529.2 kbits/s. Dependendo do material a ser comprimido e desta taxa, o processo pode ser sem perdas.
Exemplo: Dolby ADM (Adaptive Delta Modulation)
II.3 - Adaptive Differential Coding (ADPCM)
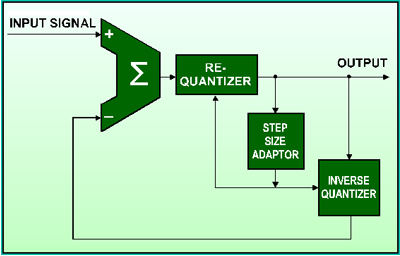
Nesta técnica, a codificação da diferença entre amostras consecutivas é feita de forma não linear, ou seja, Adaptativa, pois o valor do degrau de quantização é variável. No encoder, um certo numero de amostras anteriores é considerado, a nível de comportamento do sinal (slope) de forma a determinar o valor corrente do degrau (step). A função de transferência no decoder que determina os pontos de troca do valor do step é controlada pelo numero de 1’s ou 0’s consecutivos no string de dados.
Nesta técnica, a forma de aplicação mais simplista, transforma as diferenças em um string continuo de bits, cuja taxa (bits/segundo) determinará a taxa de compressão do processo. Nesta filosofia a taxa do string de bits e seus valores estão mais vinculados a visão linear ou “analógica” da forma de onda do que das amostras discretas e sua frequência de amostragem. Tomemos um exemplo hipotético de um sinal de áudio 16 bits stereo 44.1kHz comprimido em ADPCM e transmitido em uma taxa de 384 kbits/s. A taxa de transmissão minima necessária do nosso sinal sem compressão é 16 bits x 2 canais x 44.1 kHz = 1411,2 kbits/s, logo a taxa de compressão será de 1411,2 / 384 = 3,675. A relação bit/amostra é de 192 / 44.1 = 4,35… , ou seja, um valor não inteiro que pressupõe um processo de oversampling e conversão de sample rate, processos estes que recalculam o slope do sinal, ou seja o seu comportamento linear para realizar a operação desejada.
Exemplo: APTX
CD-I (4 bits ADPCM = SNR 60dB em bandas de 17 kHz e 8.5 kHz
8 bits ADPCM = SNR 90dB em 17 kHz)
Nesta técnica, a codificação da diferença entre amostras consecutivas é feita de forma não linear, ou seja, Adaptativa, pois o valor do degrau de quantização é variável. No encoder, um certo numero de amostras anteriores é considerado, a nível de comportamento do sinal (slope) de forma a determinar o valor corrente do degrau (step). A função de transferência no decoder que determina os pontos de troca do valor do step é controlada pelo numero de 1’s ou 0’s consecutivos no string de dados.
Nesta técnica, a forma de aplicação mais simplista, transforma as diferenças em um string continuo de bits, cuja taxa (bits/segundo) determinará a taxa de compressão do processo. Nesta filosofia a taxa do string de bits e seus valores estão mais vinculados a visão linear ou “analógica” da forma de onda do que das amostras discretas e sua frequência de amostragem. Tomemos um exemplo hipotético de um sinal de áudio 16 bits stereo 44.1kHz comprimido em ADPCM e transmitido em uma taxa de 384 kbits/s. A taxa de transmissão minima necessária do nosso sinal sem compressão é 16 bits x 2 canais x 44.1 kHz = 1411,2 kbits/s, logo a taxa de compressão será de 1411,2 / 384 = 3,675. A relação bit/amostra é de 192 / 44.1 = 4,35… , ou seja, um valor não inteiro que pressupõe um processo de oversampling e conversão de sample rate, processos estes que recalculam o slope do sinal, ou seja o seu comportamento linear para realizar a operação desejada.
Exemplo: APTX
CD-I (4 bits ADPCM = SNR 60dB em bandas de 17 kHz e 8.5 kHz
8 bits ADPCM = SNR 90dB em 17 kHz)
II.4 - Floating Point Coding & Floating Point Block Coding
Na codificação tipo Floating Point, o sinal é codificado na forma de um expoente de base 2 e uma mantissa. Fica claro que a relação sinal/ruído está amarrada ao numero de bits desta mantissa. A técnica de compressão conhecida como Floating Point Block Coding agrupa o maior numero possível de amostras sucessivas com mesmo expoente, assemblando um bloco de x mantissas para um único expoente.
Exemplo: NICAM 728 (amostras de 14 bits são transformadas em blocos de 32 mantissas de 10 bits com um único expoente de 3 bits, onde cada bit representa um degrau de 6dB).
Revisando os conceitos: A codificação PCM, já tão difundida, toma o sinal analógico e o codifica matemáticamente (converte) em um numero fixo de bits, presentemente 16~24 bits, onde sinais maiores são representados por numeros maiores e sinais menores representados por numeros menores. Ficou um tanto abstrato, não é? Vamos a um exemplo para clarificar. Tomemos um sinal senoidal com nivel de 0dB de fundo de escala. Como o bit mais significativo representa o sinal ( se zero é positivo, se 1 é negativo), se codificarmos esta senóide com 16 bits, o valor do pico positivo será de 2 elevado a 15 menos 1, ou seja 32.767. Para uma senoide à -40 dB de fundo de escala ( 100 vezes menor ) seu pico positivo valerá 327. Ou seja, quanto menor o sinal menos definição e precisão ( coisa que ocorre igualmente e na mesma proporção em meio analógico, devido ao nivel de ruído e distorções ). Esta forma matemática de codificação chama-se Ponto Fixo.
Imaginemos uma máquina de cálculo que só possuisse 4 digitos. Ela pode apresentar valores de 1 à 9999 se a vírgula estiver fixa a direita, porém se a vírgula puder se mover então poderá representar numeros de 0,001 à 9999. Neste caso a sensibilidade de cálculo é muito maior, mesmo com apenas 4 casas de precisão. No primeiro caso o menor numero codificável é o 1 e no segundo é 0,001, ou seja, um numero 1000 vezes menor! Este exemplo é uma apresentação simplificada da codificação em Ponto Flutuante ( não esquecer que no USA a vírgula é representada pelo ponto). Como é que na prática realiza-se esta representação? Separa-se uma certa quantidade de dígitos para codificar a posição da vírgula, no caso decimal a potência de 10 (no caso digital ou binário a potência de 2) , e o restante dos dígitos codificam um numero. Logo, por exemplo, o numero 957 poderia ser codificado como 3.957 = 10 elevado a terceira x 0,957. Da mesma forma que o numero 9,57 seria codificado como 1.957 = 10 x 0,957. Ou seja, determinada a ordem de grandeza (potência de 10) o valor de codificação naquela ordem tem precisão de 3 dígitos, logo esta forma nos permite codificar numeros menores com maior precisão ou sensibilidade. Como podemos ver, a codificação em ponto flutuante opera por faixas, determinadas pela potência da base numérica, logo o ruído de quantização também será determinado por faixas e proporcional a largura da mantissa. Isto significa: Para sinais maiores, maior ruído de quantização, para sinais menores, menor ruído. Por consequência, é possivel a codificação de baixos sinais com baixo ruído.
Logo qual o conceito básico da técnica de compressão Floating Point? Fixa-se o valor do ruído e distorção de quantização aceitável para as faixas, por exemplo 72 dB. Com isto definimos nossa mantissa com 12 bits. Somando-se o bit de sinal e agregando-se mais 3 bits para expoente acabamos de codificar um sinal de 24 bits em 16 bits, mantendo a mesma qualidade, relação sinal/Ruído e definição na faixa de sinais mais baixos!
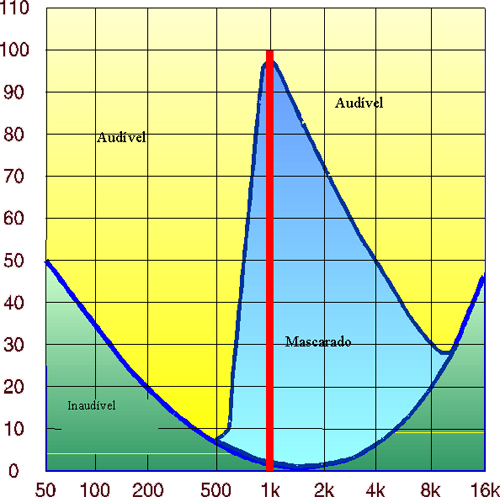
II.5 - Masking
Esta técnica leva em conta as características de mascaramento em frequência e tempo do sistema auditivo humano. Basicamente quando existem dois sinais com freqüências próximas e com uma grande relação de nível entre si, o sistema auditivo humano se encarrega de “eliminar” (mascarar) o sinal mais baixo. Normalmente é utilizada em conjunto com outras formas de codificação. O segredo desta forma de codificação está na qualidade do modelo matemático que implementa o sistema auditivo humano. Obviamente quanto mais complexo, mais próximo chega do ideal, porém as limitações desta modelagem são determinadas, em grande parte, pelo poder de processamento em tempo real dos DSP’s atuais. É claro que um sistema implementado corretamente poderia ser considerado sem perdas, pois, a presença ou ausência de elementos sonoros nunca audíveis é irrelevante. De forma um tanto radical, ao escutarmos ao vivo um show do Metalica ou a Sinfônica de Berlim, o ruido dos cupins no palco é realmente irrelevante por ser absolutamente imperceptível. Esta técnica corretamente aplicada em conjunto com outras pode possibilitar uma enorme redução de bit rate, liberando dados para uma melhor codificação dos elementos efetivamente importantes.
Exemplo: APTX, Dolby AC-2/3, PASC, ATRAC, MUSICAM, ASPEC, ISO/MPEG
Na codificação tipo Floating Point, o sinal é codificado na forma de um expoente de base 2 e uma mantissa. Fica claro que a relação sinal/ruído está amarrada ao numero de bits desta mantissa. A técnica de compressão conhecida como Floating Point Block Coding agrupa o maior numero possível de amostras sucessivas com mesmo expoente, assemblando um bloco de x mantissas para um único expoente.
Exemplo: NICAM 728 (amostras de 14 bits são transformadas em blocos de 32 mantissas de 10 bits com um único expoente de 3 bits, onde cada bit representa um degrau de 6dB).
Revisando os conceitos: A codificação PCM, já tão difundida, toma o sinal analógico e o codifica matemáticamente (converte) em um numero fixo de bits, presentemente 16~24 bits, onde sinais maiores são representados por numeros maiores e sinais menores representados por numeros menores. Ficou um tanto abstrato, não é? Vamos a um exemplo para clarificar. Tomemos um sinal senoidal com nivel de 0dB de fundo de escala. Como o bit mais significativo representa o sinal ( se zero é positivo, se 1 é negativo), se codificarmos esta senóide com 16 bits, o valor do pico positivo será de 2 elevado a 15 menos 1, ou seja 32.767. Para uma senoide à -40 dB de fundo de escala ( 100 vezes menor ) seu pico positivo valerá 327. Ou seja, quanto menor o sinal menos definição e precisão ( coisa que ocorre igualmente e na mesma proporção em meio analógico, devido ao nivel de ruído e distorções ). Esta forma matemática de codificação chama-se Ponto Fixo.
Imaginemos uma máquina de cálculo que só possuisse 4 digitos. Ela pode apresentar valores de 1 à 9999 se a vírgula estiver fixa a direita, porém se a vírgula puder se mover então poderá representar numeros de 0,001 à 9999. Neste caso a sensibilidade de cálculo é muito maior, mesmo com apenas 4 casas de precisão. No primeiro caso o menor numero codificável é o 1 e no segundo é 0,001, ou seja, um numero 1000 vezes menor! Este exemplo é uma apresentação simplificada da codificação em Ponto Flutuante ( não esquecer que no USA a vírgula é representada pelo ponto). Como é que na prática realiza-se esta representação? Separa-se uma certa quantidade de dígitos para codificar a posição da vírgula, no caso decimal a potência de 10 (no caso digital ou binário a potência de 2) , e o restante dos dígitos codificam um numero. Logo, por exemplo, o numero 957 poderia ser codificado como 3.957 = 10 elevado a terceira x 0,957. Da mesma forma que o numero 9,57 seria codificado como 1.957 = 10 x 0,957. Ou seja, determinada a ordem de grandeza (potência de 10) o valor de codificação naquela ordem tem precisão de 3 dígitos, logo esta forma nos permite codificar numeros menores com maior precisão ou sensibilidade. Como podemos ver, a codificação em ponto flutuante opera por faixas, determinadas pela potência da base numérica, logo o ruído de quantização também será determinado por faixas e proporcional a largura da mantissa. Isto significa: Para sinais maiores, maior ruído de quantização, para sinais menores, menor ruído. Por consequência, é possivel a codificação de baixos sinais com baixo ruído.
Logo qual o conceito básico da técnica de compressão Floating Point? Fixa-se o valor do ruído e distorção de quantização aceitável para as faixas, por exemplo 72 dB. Com isto definimos nossa mantissa com 12 bits. Somando-se o bit de sinal e agregando-se mais 3 bits para expoente acabamos de codificar um sinal de 24 bits em 16 bits, mantendo a mesma qualidade, relação sinal/Ruído e definição na faixa de sinais mais baixos!
II.5 - Masking
Esta técnica leva em conta as características de mascaramento em frequência e tempo do sistema auditivo humano. Basicamente quando existem dois sinais com freqüências próximas e com uma grande relação de nível entre si, o sistema auditivo humano se encarrega de “eliminar” (mascarar) o sinal mais baixo. Normalmente é utilizada em conjunto com outras formas de codificação. O segredo desta forma de codificação está na qualidade do modelo matemático que implementa o sistema auditivo humano. Obviamente quanto mais complexo, mais próximo chega do ideal, porém as limitações desta modelagem são determinadas, em grande parte, pelo poder de processamento em tempo real dos DSP’s atuais. É claro que um sistema implementado corretamente poderia ser considerado sem perdas, pois, a presença ou ausência de elementos sonoros nunca audíveis é irrelevante. De forma um tanto radical, ao escutarmos ao vivo um show do Metalica ou a Sinfônica de Berlim, o ruido dos cupins no palco é realmente irrelevante por ser absolutamente imperceptível. Esta técnica corretamente aplicada em conjunto com outras pode possibilitar uma enorme redução de bit rate, liberando dados para uma melhor codificação dos elementos efetivamente importantes.
Exemplo: APTX, Dolby AC-2/3, PASC, ATRAC, MUSICAM, ASPEC, ISO/MPEG
II.6 - Linear & Adaptive Predictive Coding
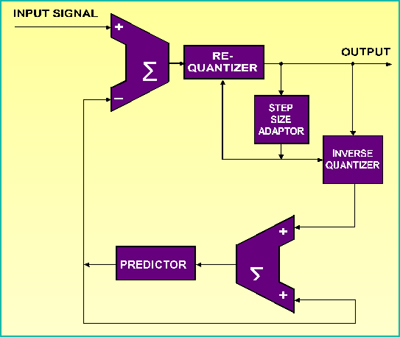
As técnicas de predição se assemelham aos moduladores Sigma-Delta e as técnicas diferenciais. Um certo bloco de amostras é processado e o valor da amostra seguinte é avaliado. A diferença entre esta amostra e o valor avaliado é então requantizado (comprimido). Com o intuito de reduzir o erro de requantização (compressão), a saída do processo entra num quantizador inverso e é combinado com a amostra avaliada, gerando assim a próxima entrada do bloco de avaliação, tendo já embutido em seu valor, o erro de requantização. Quando o valor da saída (diferença) é pequeno, dizemos que o Bloco Avaliador antecipou o valor seguinte, por esta razão, chamado de Predictive Coding. A Predição é dita também Adaptativa quando o step de requantização é variável em função do slope do sinal. Este tipo de técnica possui a vantagem de processar a forma de onda no domínio do tempo, logo utilizando blocos de amostras relativamente pequenos, gerando assim um delay de processamento relativamente curto. Uma outra vantagem reside no fato que dados diferenciais são menos sensíveis a bit errors que o PCM Linear, em virtude destes sinais representarem apenas uma parte da amplitude final do sinal.
Agora o dado a ser transmitido é a diferença entre a amostra atual e a amostra predita. Como já dissemos anteriormente, o áudio possui alta correlação entre amostras consecutivas, desta forma, se o modelo de predição possuir complexidade suficiente para quantificar apropriadamente todas as características físicas e fenomênicas do evento áudio, esta predição pode chegar a uma precisão quase ideal tornando a diferença a ser requantizada mínima, próxima a zero, permitindo altas taxas de compressão, sem perdas.
As técnicas de predição se assemelham aos moduladores Sigma-Delta e as técnicas diferenciais. Um certo bloco de amostras é processado e o valor da amostra seguinte é avaliado. A diferença entre esta amostra e o valor avaliado é então requantizado (comprimido). Com o intuito de reduzir o erro de requantização (compressão), a saída do processo entra num quantizador inverso e é combinado com a amostra avaliada, gerando assim a próxima entrada do bloco de avaliação, tendo já embutido em seu valor, o erro de requantização. Quando o valor da saída (diferença) é pequeno, dizemos que o Bloco Avaliador antecipou o valor seguinte, por esta razão, chamado de Predictive Coding. A Predição é dita também Adaptativa quando o step de requantização é variável em função do slope do sinal. Este tipo de técnica possui a vantagem de processar a forma de onda no domínio do tempo, logo utilizando blocos de amostras relativamente pequenos, gerando assim um delay de processamento relativamente curto. Uma outra vantagem reside no fato que dados diferenciais são menos sensíveis a bit errors que o PCM Linear, em virtude destes sinais representarem apenas uma parte da amplitude final do sinal.
Agora o dado a ser transmitido é a diferença entre a amostra atual e a amostra predita. Como já dissemos anteriormente, o áudio possui alta correlação entre amostras consecutivas, desta forma, se o modelo de predição possuir complexidade suficiente para quantificar apropriadamente todas as características físicas e fenomênicas do evento áudio, esta predição pode chegar a uma precisão quase ideal tornando a diferença a ser requantizada mínima, próxima a zero, permitindo altas taxas de compressão, sem perdas.
II.7 - Sub Band Coding
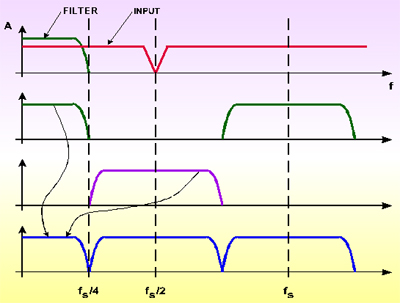
A técnica Sub Band Data Reduction vale-se do fato do áudio não possuir distribuição espectral uniforme de energia. No caso do PCM, todo o range dinâmico é ocupado pela componente espectral mais forte e as demais componentes são codificadas como excesso de Headroom. Basicamente, o espectro é subdividido em diversas bandas e cada banda é codificada de acordo com sua energia. O numero de bandas é determinado pela técnica de redução utilizada. O processo de subdivisão do espectro é complicado e exige um processamento pesado. Um método muito utilizado é o de Quadrature Mirror Fitering, ou simplesmente QMF. O QMF é uma espécie de Filtro FIR que converte um string de amostras PCM em dois strings (um para cada metade do espectro) cada um com metade do sampling rate, mantendo assim a taxa de saída igual a de entrada. A parte superior do espectro é heterodinada para baixo de forma a coincidir com a parte inferior, reduzindo assim a banda à metade, permitindo a decimação de um fator de 2. Um numero maior de bandas é obtido associando-se QMF’s numa estrutura de árvore.
Em virtude da decimação, metade do esforço computacional é jogado fora, e para economizar este precioso tempo, usa-se como alternativa os Polyphase Pseudo-QMF filters ou Wave Filters, nos quais os processos de filtragem e decimação são combinados. Somente as amostras desejadas são computadas. Como podemos ver, o método de QMF gera bandas de mesma largura, enquanto que as bandas críticas de audição possuem largura não uniforme. Se a técnica de Masking for utilizada em conjunto com Sub Band Coding, os modelos de mascaramento precisam ser recalculados, e mesmo assim, consegue-se uma taxa de compressão um pouco menor que se as bandas obtidas fossem coincidentes com as bandas críticas.
A combinação da SBC com Masking permite um ganho de código enorme, visto que cada banda já é codificada levando em consideração a energia nela contida, e consequentemente o numero de bits utilizados para requantizá-la é determinado por esta quantidade de energia, o Mascaramento a reduz ainda mais eliminando componentes e bandas qualificadas como inaudíveis. Mais uma vêz vale a pena ressaltar que o processamento próximo ao ideal pode levar a taxas de compressão elevadas e um resultado avaliado como sem perdas.
QMF
A técnica Sub Band Data Reduction vale-se do fato do áudio não possuir distribuição espectral uniforme de energia. No caso do PCM, todo o range dinâmico é ocupado pela componente espectral mais forte e as demais componentes são codificadas como excesso de Headroom. Basicamente, o espectro é subdividido em diversas bandas e cada banda é codificada de acordo com sua energia. O numero de bandas é determinado pela técnica de redução utilizada. O processo de subdivisão do espectro é complicado e exige um processamento pesado. Um método muito utilizado é o de Quadrature Mirror Fitering, ou simplesmente QMF. O QMF é uma espécie de Filtro FIR que converte um string de amostras PCM em dois strings (um para cada metade do espectro) cada um com metade do sampling rate, mantendo assim a taxa de saída igual a de entrada. A parte superior do espectro é heterodinada para baixo de forma a coincidir com a parte inferior, reduzindo assim a banda à metade, permitindo a decimação de um fator de 2. Um numero maior de bandas é obtido associando-se QMF’s numa estrutura de árvore.
Em virtude da decimação, metade do esforço computacional é jogado fora, e para economizar este precioso tempo, usa-se como alternativa os Polyphase Pseudo-QMF filters ou Wave Filters, nos quais os processos de filtragem e decimação são combinados. Somente as amostras desejadas são computadas. Como podemos ver, o método de QMF gera bandas de mesma largura, enquanto que as bandas críticas de audição possuem largura não uniforme. Se a técnica de Masking for utilizada em conjunto com Sub Band Coding, os modelos de mascaramento precisam ser recalculados, e mesmo assim, consegue-se uma taxa de compressão um pouco menor que se as bandas obtidas fossem coincidentes com as bandas críticas.
A combinação da SBC com Masking permite um ganho de código enorme, visto que cada banda já é codificada levando em consideração a energia nela contida, e consequentemente o numero de bits utilizados para requantizá-la é determinado por esta quantidade de energia, o Mascaramento a reduz ainda mais eliminando componentes e bandas qualificadas como inaudíveis. Mais uma vêz vale a pena ressaltar que o processamento próximo ao ideal pode levar a taxas de compressão elevadas e um resultado avaliado como sem perdas.
QMF
II.8 - Transform Coding (Spectral Coding)
A transformada de Fourier de um sinal de Áudio, ou seja, uma forma de onda no domínio do tempo, apresenta as frequências componentes deste sinal, seus slopes e fases. No domínio da frequência, estes parâmetros mudam mais lentamente, ou seja, são mais previsíveis, o que naturalmente representa um ganho de código. Devido a limitação imposta pelo Coding Delay (intervalo de tempo necessário para realizar a codificação), o sinal de áudio tem que ser sub dividido em blocos de amostras e transformados individualmente. Para solucionar os diversos problemas provenientes desta segmentação, várias técnicas foram desenvolvidas, sendo uma das mais utilizadas a MDCT ( Modified Discrete Cosine Transform). Esta transformada faz uso de Overlapped Cosine Windows, que geram o dobro de coeficientes. Estes coeficientes são decimados num fator de dois, o que potencialmente geraria Aliasing no domínio da frequência, porém ao se realizar a transformada inversa, as componentes alias se apresentam com polaridade invertida de uma janela para outra, cancelando-se. Este principio é chamado de TDAC (Time Domain Aliasing Cancellation). Um outro artificio utilizado para diminuir o ruído gerado quando um bloco de dados (janela) termina com um transiente, é a utilização de janelas adaptativas (blocos de comprimento variável).
A Transform Coding possui suficiente resolução para controlar o modelo de mascaramento diretamente e a Equal Width Sub Band Coding possui melhor resolução de frequência nos bancos de filtro de forma a obter um melhor ganho na redução de código, porém é pobre no que diz respeito ao modelo perceptual (Masking), particularmente na curva do lado das baixas frequências do mascarador. A combinação dos dois modelos aumenta consideravelmente a capacidade de redução de código, reduzindo ao mesmo tempo a complexidade dos mesmos.
II.9 – Lossless Coding (AUDIO DATA PACKING)
Diversas filosofias e algoritmos foram desenvolvidos ( AptX, AptQ, AC-2, AC-3, PASC, ATRAC, MUSICAM, ASPEC, ISO/MPEG’s …) , sendo atualmente utilizados principalmente na transmissão digital, visto que todos, sem exceção, possuem uma desvantagem em comum (cada um num certo grau e característica): Não são transparentes, ou seja, possuem perdas e geram distorções diversas. No Áudio profissional estes fatores são decisivos na aceitação ou não de um dado processo visto que a alegação básica utilizada pelos defensores do áudio digital é uma pureza e cristalinidade cada vez maior com o avanço da tecnologia. Nos dias de hoje onde os 16 bits de quantização e sample rate de 44.1kHz já são vistos como ultrapassados e fala-se de 24 bits à 96kHz (ou mesmo 192kHz) de frequência de amostragem, os audiófilos e engenheiros de estúdio torcem o nariz a mais tênue possibilidade de compressão, que é vista como retrocesso. Óbviamente estes conceitos são um pouco mais sutis e as diversas alegações devem ser avaliadas de forma mais cuidadosa e impessoal.
Porém, para todo problema existe sempre alguém buscando solução. Existe atualmente uma corrente de pesquisa desenvolvendo teorias e algoritmos chamados de Lossless, ou seja, sem perdas. Os processos de Lossless Data Compression, preferencialmente chamados de PACKING (Compactação - para evitar associações aos processos de compressão com perdas) , não elimina nenhuma informação do sinal, apenas reagrupa os dados de maneira mais eficiente através do canal de dados disponível, permitindo assim a reconstituição exata do sinal original.
Princípios de Packing
Acredito que praticamente todos os leitores estão familiarizados com os aplicativos de packing utilizados em computadores, como por exemplo o PKZIP e/ou WINZIP, que em média comprime arquivos à 50% de seu tamanho. Basicamente este tipo de aplicativo reordena os dados levando em consideração as redundâncias presentes (redundâncias de bits, nibbles, bytes & words) reformatando (ou seja, reorganizando blocos de dados em um outro formato) para desta forma reduzir o volume ocupado. O PCM standard, o mais largamente utilizado formato de representação de áudio, não é necessariamente o mais eficiente para todos os casos. O Packing pode ser visto como um processo de reformatação mais eficiente de dados de forma a obter uma maior economia do canal, fazendo uso, por exemplo, das técnicas de redução de redundâncias presentes na representação standard PCM, convertendo-a para um formato no qual as redundâncias são minimizadas. De forma geral, um encoder Packing toma uma dada forma de onda representada por uma palavra de vários bits e a transforma, de forma reversível em uma outra com uma palavra de comprimento menor que pode ser transmitida através de um dado canal numa taxa também menor. Na recepção o decoder usa a transformada inversa do processo, reconstituindo o sinal original em sua integra.
Tomemos como exemplo os dados da tabela 1, que é a representação de uma porção de uma senóide de 4kHz à -50dB amostrada com 20 bits a 48kHz.
Tabela 1
Amostra Valor Binário
1 00000000010000110000
2 00000000011000010000
3 00000000011001100000
4 00000000010011110000
5 00000000001000110000
6 11111111111011100000
7 11111111101111010000
8 11111111100111110000
9 11111111100110100000
10 11111111101100010000
11 11111111110111010000
12 00000000000100100000
As 12 amostras ocupam um total de 240 bits. Logo à primeira observação notamos que os quatro bits menos significativos são nulos, caracterizando claramente que trata-se de um sinal de 16 bits transmitido em um canal de 20 bits. Um encoder que detectasse este fato necessitaria apenas inserir no header do bloco de dados a informação de que iria transmitir apenas os 16 bits mais significativos e desta forma já estaria economizando 20% no data rate. Notamos também que os 9 bits superiores ou são zeros ou 1’s, como seria de se esperar de um sinal com baixo nível (-50dB). Se o decoder for capaz de codificar esta outra característica basta transmitir 8 bits a partir do nono, o que representa uma redução de 60%!Na prática usa-se transmitir os dados em blocos, com comprimento típico em torno de 500 amostras (10 mS). Cada bloco é processado separadamente, contendo em seu header todas as informações necessárias para tal. Blocos muito longos podem apresentar nuances de nível e até momentos de silencio que reduziriam a capacidade de compactação, enquanto que blocos muito curtos tem a desvantagem do overhead de dados contidos no header do bloco, levando-nos a um bloco típico de 10mS.
Métodos de Predição
Está claro que não podemos ir muito mais além , em termos de redução de redundâncias, do que o exemplo acima, que se torna muito eficaz para passagens clássicas de baixo nível porém já não gera grandes ganhos em gravações de pop ou rock onde se utiliza largamente compressão dinâmica.
Como obtermos maiores índices de compactação? O segredo está na diferença…
Agora, na otimização do processo, começamos a lançar mão de outras filosofias, no caso, a Differential Coding. As amostras de 16 bits do exemplo da tabela 1 tem como valores decimais +67, +97,+102, +79, +35, -18, -67, -97, -102,-79, -35, +18, e a diferença entre pares sucessivos de números é +30, +5, -23, -44, -53, -49, -30, -5, +23, +44, e +53. Se transmitirmos o primeiro numero do bloco no header (+67), bastará transmitir as diferenças para que possamos reconstituir todo o bloco na recepção. Nesta operação ganhamos um bit, que no exemplo parece não ser grande coisa, porém se a senóide fosse de 400Hz ao invés de 4kHz, a redução seria de 8 para 4 bits, o que representa 50%! O exemplo acima é a forma mais simples de predição possível com um preditor de primeira ordem. Se nós partíssemos para a diferença da diferença (2a. ordem) menos bits seriam necessários para codificarmos o bloco. Neste ponto nos sentimos tentados a partir para ordens maiores no filtro de predição, porém, evitando longas demonstrações matemáticas, o que determina e limita a ordem do filtro de predição é o conteúdo de alta frequência do sinal de áudio. Preditores de ordem elevada tem componentes do ruído de quantização amplificados a um ponto que ultrapassam o próprio sinal. Por razões como esta, em termos práticos, raramente pode-se ir além de preditores de 3a. ordem.
A transformada de Fourier de um sinal de Áudio, ou seja, uma forma de onda no domínio do tempo, apresenta as frequências componentes deste sinal, seus slopes e fases. No domínio da frequência, estes parâmetros mudam mais lentamente, ou seja, são mais previsíveis, o que naturalmente representa um ganho de código. Devido a limitação imposta pelo Coding Delay (intervalo de tempo necessário para realizar a codificação), o sinal de áudio tem que ser sub dividido em blocos de amostras e transformados individualmente. Para solucionar os diversos problemas provenientes desta segmentação, várias técnicas foram desenvolvidas, sendo uma das mais utilizadas a MDCT ( Modified Discrete Cosine Transform). Esta transformada faz uso de Overlapped Cosine Windows, que geram o dobro de coeficientes. Estes coeficientes são decimados num fator de dois, o que potencialmente geraria Aliasing no domínio da frequência, porém ao se realizar a transformada inversa, as componentes alias se apresentam com polaridade invertida de uma janela para outra, cancelando-se. Este principio é chamado de TDAC (Time Domain Aliasing Cancellation). Um outro artificio utilizado para diminuir o ruído gerado quando um bloco de dados (janela) termina com um transiente, é a utilização de janelas adaptativas (blocos de comprimento variável).
A Transform Coding possui suficiente resolução para controlar o modelo de mascaramento diretamente e a Equal Width Sub Band Coding possui melhor resolução de frequência nos bancos de filtro de forma a obter um melhor ganho na redução de código, porém é pobre no que diz respeito ao modelo perceptual (Masking), particularmente na curva do lado das baixas frequências do mascarador. A combinação dos dois modelos aumenta consideravelmente a capacidade de redução de código, reduzindo ao mesmo tempo a complexidade dos mesmos.
II.9 – Lossless Coding (AUDIO DATA PACKING)
Diversas filosofias e algoritmos foram desenvolvidos ( AptX, AptQ, AC-2, AC-3, PASC, ATRAC, MUSICAM, ASPEC, ISO/MPEG’s …) , sendo atualmente utilizados principalmente na transmissão digital, visto que todos, sem exceção, possuem uma desvantagem em comum (cada um num certo grau e característica): Não são transparentes, ou seja, possuem perdas e geram distorções diversas. No Áudio profissional estes fatores são decisivos na aceitação ou não de um dado processo visto que a alegação básica utilizada pelos defensores do áudio digital é uma pureza e cristalinidade cada vez maior com o avanço da tecnologia. Nos dias de hoje onde os 16 bits de quantização e sample rate de 44.1kHz já são vistos como ultrapassados e fala-se de 24 bits à 96kHz (ou mesmo 192kHz) de frequência de amostragem, os audiófilos e engenheiros de estúdio torcem o nariz a mais tênue possibilidade de compressão, que é vista como retrocesso. Óbviamente estes conceitos são um pouco mais sutis e as diversas alegações devem ser avaliadas de forma mais cuidadosa e impessoal.
Porém, para todo problema existe sempre alguém buscando solução. Existe atualmente uma corrente de pesquisa desenvolvendo teorias e algoritmos chamados de Lossless, ou seja, sem perdas. Os processos de Lossless Data Compression, preferencialmente chamados de PACKING (Compactação - para evitar associações aos processos de compressão com perdas) , não elimina nenhuma informação do sinal, apenas reagrupa os dados de maneira mais eficiente através do canal de dados disponível, permitindo assim a reconstituição exata do sinal original.
Princípios de Packing
Acredito que praticamente todos os leitores estão familiarizados com os aplicativos de packing utilizados em computadores, como por exemplo o PKZIP e/ou WINZIP, que em média comprime arquivos à 50% de seu tamanho. Basicamente este tipo de aplicativo reordena os dados levando em consideração as redundâncias presentes (redundâncias de bits, nibbles, bytes & words) reformatando (ou seja, reorganizando blocos de dados em um outro formato) para desta forma reduzir o volume ocupado. O PCM standard, o mais largamente utilizado formato de representação de áudio, não é necessariamente o mais eficiente para todos os casos. O Packing pode ser visto como um processo de reformatação mais eficiente de dados de forma a obter uma maior economia do canal, fazendo uso, por exemplo, das técnicas de redução de redundâncias presentes na representação standard PCM, convertendo-a para um formato no qual as redundâncias são minimizadas. De forma geral, um encoder Packing toma uma dada forma de onda representada por uma palavra de vários bits e a transforma, de forma reversível em uma outra com uma palavra de comprimento menor que pode ser transmitida através de um dado canal numa taxa também menor. Na recepção o decoder usa a transformada inversa do processo, reconstituindo o sinal original em sua integra.
Tomemos como exemplo os dados da tabela 1, que é a representação de uma porção de uma senóide de 4kHz à -50dB amostrada com 20 bits a 48kHz.
Tabela 1
Amostra Valor Binário
1 00000000010000110000
2 00000000011000010000
3 00000000011001100000
4 00000000010011110000
5 00000000001000110000
6 11111111111011100000
7 11111111101111010000
8 11111111100111110000
9 11111111100110100000
10 11111111101100010000
11 11111111110111010000
12 00000000000100100000
As 12 amostras ocupam um total de 240 bits. Logo à primeira observação notamos que os quatro bits menos significativos são nulos, caracterizando claramente que trata-se de um sinal de 16 bits transmitido em um canal de 20 bits. Um encoder que detectasse este fato necessitaria apenas inserir no header do bloco de dados a informação de que iria transmitir apenas os 16 bits mais significativos e desta forma já estaria economizando 20% no data rate. Notamos também que os 9 bits superiores ou são zeros ou 1’s, como seria de se esperar de um sinal com baixo nível (-50dB). Se o decoder for capaz de codificar esta outra característica basta transmitir 8 bits a partir do nono, o que representa uma redução de 60%!Na prática usa-se transmitir os dados em blocos, com comprimento típico em torno de 500 amostras (10 mS). Cada bloco é processado separadamente, contendo em seu header todas as informações necessárias para tal. Blocos muito longos podem apresentar nuances de nível e até momentos de silencio que reduziriam a capacidade de compactação, enquanto que blocos muito curtos tem a desvantagem do overhead de dados contidos no header do bloco, levando-nos a um bloco típico de 10mS.
Métodos de Predição
Está claro que não podemos ir muito mais além , em termos de redução de redundâncias, do que o exemplo acima, que se torna muito eficaz para passagens clássicas de baixo nível porém já não gera grandes ganhos em gravações de pop ou rock onde se utiliza largamente compressão dinâmica.
Como obtermos maiores índices de compactação? O segredo está na diferença…
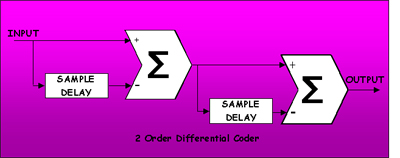
Agora, na otimização do processo, começamos a lançar mão de outras filosofias, no caso, a Differential Coding. As amostras de 16 bits do exemplo da tabela 1 tem como valores decimais +67, +97,+102, +79, +35, -18, -67, -97, -102,-79, -35, +18, e a diferença entre pares sucessivos de números é +30, +5, -23, -44, -53, -49, -30, -5, +23, +44, e +53. Se transmitirmos o primeiro numero do bloco no header (+67), bastará transmitir as diferenças para que possamos reconstituir todo o bloco na recepção. Nesta operação ganhamos um bit, que no exemplo parece não ser grande coisa, porém se a senóide fosse de 400Hz ao invés de 4kHz, a redução seria de 8 para 4 bits, o que representa 50%! O exemplo acima é a forma mais simples de predição possível com um preditor de primeira ordem. Se nós partíssemos para a diferença da diferença (2a. ordem) menos bits seriam necessários para codificarmos o bloco. Neste ponto nos sentimos tentados a partir para ordens maiores no filtro de predição, porém, evitando longas demonstrações matemáticas, o que determina e limita a ordem do filtro de predição é o conteúdo de alta frequência do sinal de áudio. Preditores de ordem elevada tem componentes do ruído de quantização amplificados a um ponto que ultrapassam o próprio sinal. Por razões como esta, em termos práticos, raramente pode-se ir além de preditores de 3a. ordem.
A idéia básica de um preditor ideal é de que ao predizermos através de um dado algoritmo (equação), o sinal-diferença gerado é o menor possível, precisando de pouquíssimos bits para codificá-lo. No exemplo anterior usamos preditores diferenciais simples, porque então não partirmos para preditores mais complexos? Estudos realizados utilizando filtros de predição a base de IIR e FIR filters mostraram que preditores utilizando IIR são mais simples e de ordem menor que os a base de FIR devido ao extremamente largo range dinâmico necessário ao áudio de alta qualidade, onde muitas vezes encontramos componentes do espectro com diferenças de 60 à 80dB entre si. Imaginemos agora um Encoder capaz de, ao analisar um dado bloco, escolher o tipo e a ordem do filtro mais apropriada para codificar estes dados. Seria necessário apenas enviar no header do bloco os parâmetros e tipo do filtro de predição e o Decoder se encarregaria de reconstruir o bloco. Se os filtros fossem tabelados, bastaria mandar o endereço da tabela que define o filtro selecionado! Melhor que isto, impossível.
Métodos de correção
Uma forma alternativa de Packing seria utilizar-se uma das já tão aceitas e testadas técnicas de compressão existentes (que como sabemos alcançam índices de compressão elevados), obtermos o erro (diferença) e o enviarmos junto com o pacote comprimido. Um processo Lossy de alta qualidade teria uma perda ou erro pequena, o que representaria um pequeno aumento a codificação apropriada desta diferença. O algoritmo “Lossy” poderia ser baseado em qualquer um dos transform-coding schemes utilizados em aplicações de Consumer Low Bit Rate , porém sem o módulo de “Psychoacoustic masking”, pois faz-se necessário que o erro tenha um espectro o mais constante possível e próximo a ruído branco para que o processo de packing do mesmo seja eficaz. Ao avaliarmos este tipo de esquema, baseado em algoritmos do tipo transform-coding, notamos serem os mesmos muito mais complexos e, obviamente mais caros que os baseados em preditores, não acrescentando grandes aumentos na compactação do áudio. A nível comercial não parecem, até o presente momento, ser uma solução muito atrativa.
Huffman Coding
Independente da nossa filosofia estar usando um esquema de predição ou de correção, nós teremos uma diferença ou um erro para ser transmitido, e como o sinal é tratado na base de blocos, é desejável que o bloco a ser transmitido use o menor numero de bits possível. Apesar dos sinais de áudio possuírem certas características “predizíveis”, muitas vezes dentro de um bloco de dados alguns extrapolam o valor médio dos demais, e se por exemplo, o valor médio pode ser codificado com 5 bits, porque todo o bloco deve ser transmitido com 8 bits por causa de 10% dos dados?
O código de Huffman é a solução ideal para este tipo de problema. A idéia é utilizar uma Tabela de Conversão para converter os dados de entrada, que possuem numero fixo de bits em outros, de largura variável, onde dados de maior ocorrência possuem menos bits e dados de menor ocorrência possuem mais bits para sua representação. Desta forma, consegue-se, em média, transmitir-se menos bits. Tomemos o exemplo de uma distribuição de diferenças representadas por 3 bits (de -3 à +3) cuja codificação de Huffman é apresentada na Tabela 2, onde a ocorrência básica é dos valores -1, 0 e +1 e os demais valores (-3,-2,+2,+3) raramente ocorram. Fica claro que o tamanho do bloco enviado será menor, visto que o valor “0”, de maior ocorrência, é codificado com apenas um bit.
Tabela 2
Sample Value PCM Code Huffman Code
-3 101 1100
-2 110 1101
-1 111 100
0 000 0
+1 001 101
+2 010 1110
+3 011 1111
Para o áudio, cuja distribuição estatística de amplitude tende para a Laplaciana, a utilização da codificação de Huffman reduz em média 1.5 bits por amostra. Imaginemos que o Encoder trabalhe, por exemplo, com 8 bits para representar as diferenças e possua um conjunto de tabelas de codificação Huffman possíveis. Ao analisar o bloco de diferenças, escolhe a melhor tabela e envia, no header do bloco apenas a informação da tabela utilizada na codificação do bloco. O Decoder, que possui as mesmas tabelas, reconstrói o bloco de diferenças a partir da tabela selecionada passando ao preditor inverso os dados com largura constante (neste caso, 8 bits).
O sistema completo
O sistema completo proposto seria então composto de diversos blocos, onde o Decoder possuiria as funções inversas realizadas pelo Encoder. Seriam estes:
* Bloco de avaliação de redundâncias de bits (o qual reduz o comprimento médio da palavra por supressão de bits de sinal - os quais caracterizam o valor médio do bloco. Ver primeiro exemplo).
* Filtro de Predição & Tabela de filtros e/ou coeficientes de filtro
* Huffman Encoder (Decoder) & Tabelas de codificação
É óbvio que as atuais filosofias e algoritmos de Packing não chegam perto, em termos de redução de dados, das tecnologias “Lossy”, principalmente aquelas que fazem uso da psicoacústica e de mascaramento, porém é o caminho natural para o áudio de alta qualidade, que exige cada vez mais definição, pureza, detalhamento, cristalinidade, dinâmica, …
III - Modelos & Implementações
Como modelos e implementações das mencionadas, podemos citar alguns exemplos:
III.1 - apt-X100 e AptQ
III.2 - Dolby AC-2/AC-3
III.3 - PASC
III.4 - ATRAC
III.5 - MUSICAM
III.6 - ASPEC
III.7 - ISO/MPEG Layer I
III.8 - ISO/MPEG Layer II
III.9 - ISO/MPEG Layer III
III.1 - APT-X100
O Codec da Áudio Processing Technology, o APTX100, um DSP dedicado que pode ser configurado de diversas formas, usa Adaptive Predictive e Sub Band Coding (4 bandas) para obter uma taxa de compressão de 4:1. As bandas são obtidas de Quadrature Mirrors Filters, sendo implementado em cada uma um Preditor Adaptativo Continuo, eliminando a necessidade do processamento por blocos. O bloco de saída é composto de 2048 bits, começando por um pattern de sincronismo. Como o Codec processa no domínio do tempo de forma preditiva adaptativa, não é necessário um modelo preciso de mascaramento ou grande numero de bandas, resultando em um delay de processamento baixo e constante (menor que 4 mS), extremamente eficiente em aplicações em tempo real. Outra vantagem deste Codec é a grande imunidade a bit errors.
III.2 - DOLBY AC-2
O Algoritmo de Compressão AC-2 da Dolby caracteriza uma família de Transform Coders baseados em TDAC (Time Domain Aliasing Cancellation) e permite diversas configurações de delay e bit rate. O sinal de áudio passa através de uma transformada TDAC com window 50% overlapped critically sampled que faz uso de transformadas modificadas de seno e cosseno. Os coeficientes são agrupados em sub bandas aproximadamente equivalentes as bandas críticas. Os coeficientes em cada banda são normalizados e expressos na notação Floating Point Block com um único expoente. Estes expoentes nada mais são que a representação logarítmica da envoltória espectral do sinal e são utilizados pelo modelo perceptivo de mascaramento que requantiza as mantissas dos coeficientes.
III.3 - PASC
Precision Adaptive Sub-Band Coding (PASC) foi desenvolvido pela PHILIPS para ser utilizado no digital compact cassette (DCC). O PASC usa 32 Sub Bandas iguais geradas por um Polyphase QMF de 512 taps, sendo cada banda codificada via Floating Point Block. A energia do sinal em cada banda é calculada e comparada com o threshold absoluto do modelo auditivo e é então realizado o primeiro mascaramento. A quantidade de energia nas bandas acima do nível absoluto de mascaramento é computada de forma a determinar o mascaramento entre bandas, assim determinando o comprimento das mantissas em cada bloco.
III.4 - ATRAC
O ATRAC (Adaptive Transform Acoustic Coder) foi desenvolvido pela SONY e é utilizado no MiniDisk. O ATRAC usa uma combinação de Sub Band Coding com MDCT (Modified Discrete Cosine Transform) Coding. O sinal passa por um QMF que divide o espectro em duas bandas. A banda inferior passa por outro QMF que a divide em duas outras, enquanto que a banda superior passa por um delay para compensar o processamento do segundo QMF. Cada banda é formatada em blocos de amostras que são enviados a MDCT’s. O resultado das três MDCT’s são agrupados em 52 nódulos de frequência, que possuem largura de banda variável, aproximando as bandas críticas do sistema auditivo. A requantização é feita com base no modelo de mascaramento. Os blocos de amostras nos quais as bandas são formatadas, são adaptativos de forma a evitar noise pré-echo, variando de 1,45 mS (no caso de grandes transientes) até 11,6mS (quando a forma de onda do sinal é caracteristicamente estacionária). O tamanho do bloco é selecionado de forma independente em cada uma das três bandas. Este algoritmo comprime no MiniDisc um sinal de 16 bits PCM 44.1kHz na taxa de 5:1.
(Para maiores detalhes sobre o MiniDisc ou ATRAC ver artigo na revista SET n.42 Set/Out 98 de Hugo de Souza Melo)
III.5 - MUSICAM
O algoritmo MUSICAM (Masking Pattern Adapted Universal Sub-Band Integrated Coding and Mutiplex) nasceu do Projeto Eureka 147 DAB (Digital Áudio Broadcasting), fruto da associação da CCETT (França), IRT (Alemanha) e da Philips (Holanda). Este algoritmo é um misto de Sub Band Coding e Transform Coding. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. As amostras de cada banda são agrupadas em blocos de tamanho constante e igual a 12 amostras. Este tamanho de bloco foi baseado no fenômeno de pre-masking. Cada sub-band block é comprimido de acordo com o valor de pico do bloco e o mesmo possui um fator de escala de 6 bits (expoente). O modelo perceptual de mascaramento é implementado por uma FFT (Fast Fourier Transform) de 1024 pontos, resultando numa analise do espectro do sinal 8 vezes melhor que a largura de cada sub-banda. As mantissas de cada bloco são requantizadas de acordo com este modelo. Este algoritmo permite taxas de compressão entre 4:1 e 12:1, com delay de processamento de 8mS a mais de 30mS.
III.6 - ASPEC
O Algoritmo ASPEC (Adaptive Spectral Perceptual Entropy Coding) foi desenvolvido em conjunto pelo AT&T Bell Laboratories, Thomson Consumer Electronics, Fraunhofer Society e CNET visando a Norma estabelecida pelo ISO/IEC JTC1/SC2/WG11 experts group (MPEG/Áudio). Este algoritmo de compressão é baseado em Transform Coding. Uma MDCT em amostragem crítica (decimada de 2) com janelas adaptativas sobrepostas (1024 & 256 amostras respectivamente) é utilizada, sendo matematicamente equivalente a um banco de filtros de 512 bandas. Para bit rates elevados (96 e 128 kbits/s) um modelo psico-acústico simplificado é utilizado, porém para taxas de compressão maiores (bit rate de 64 kbits/s) um sofisticado modelo é implementado através de uma FFT de 1024 pontos. A requantização (compressão) dos coeficientes é implementada por um quantizador não linear, adaptativo, com base na analise temporal do erro de requantização segundo o modelo de mascaramento.
III.7 - ISO/MPEG Layer I
A ISO (International Organization for Standardization) e a IEC (International Electrotechnical Commission) em 1988 criaram o ISO/IEC/MPEG (Moving Pictures Experts Group) para o estudo, definição e estandardização dos esquemas de codificação para os futuros produtos para vídeo digital. No que se refere ao áudio, foi criado um grupo específico, o MPEG/Áudio.
O algoritmo standard ISO/MPEG Layer I é uma versão simplificada do MUSICAM. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. As amostras de cada banda são agrupadas em blocos de tamanho constante e igual a 12 amostras. Este tamanho de bloco foi baseado no fenômeno de pre-masking. Cada sub-band block é comprimido de acordo com o valor de pico do bloco e o mesmo possui um fator de escala de 6 bits (expoente). O modelo perceptual de mascaramento é obtido da analise espectral de cada banda.
III.8 - ISO/MPEG Layer II
Esta norma é idêntica a MUSICAM.
III.9 - ISO/MPEG Layer III
Este é o layer mais complexo da norma ISO. Ele só deve ser utilizado quando for necessário uma alta qualidade em taxas de transmissão muito baixas. É um algoritmo baseado em Transform Coding, misto do MUSICAM e ASPEC. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. Cada uma das bandas são processadas por um MDCT de 12 bandas de forma a obter 384 coeficientes. Dois tamanhos de janela são utilizados para mascarar o pré-echo gerado por transientes e o chaveamento destas janelas é controlado pelo modelo psico-acústico. Foi determinado que o pré-echo ocorre quando a entropia do áudio cresce acima do valor médio. Um modelo perceptual de alta precisão é implementado fazendo uso da grande resolução de frequência disponível. A requantização é não uniforme.
Métodos de correção
Uma forma alternativa de Packing seria utilizar-se uma das já tão aceitas e testadas técnicas de compressão existentes (que como sabemos alcançam índices de compressão elevados), obtermos o erro (diferença) e o enviarmos junto com o pacote comprimido. Um processo Lossy de alta qualidade teria uma perda ou erro pequena, o que representaria um pequeno aumento a codificação apropriada desta diferença. O algoritmo “Lossy” poderia ser baseado em qualquer um dos transform-coding schemes utilizados em aplicações de Consumer Low Bit Rate , porém sem o módulo de “Psychoacoustic masking”, pois faz-se necessário que o erro tenha um espectro o mais constante possível e próximo a ruído branco para que o processo de packing do mesmo seja eficaz. Ao avaliarmos este tipo de esquema, baseado em algoritmos do tipo transform-coding, notamos serem os mesmos muito mais complexos e, obviamente mais caros que os baseados em preditores, não acrescentando grandes aumentos na compactação do áudio. A nível comercial não parecem, até o presente momento, ser uma solução muito atrativa.
Huffman Coding
Independente da nossa filosofia estar usando um esquema de predição ou de correção, nós teremos uma diferença ou um erro para ser transmitido, e como o sinal é tratado na base de blocos, é desejável que o bloco a ser transmitido use o menor numero de bits possível. Apesar dos sinais de áudio possuírem certas características “predizíveis”, muitas vezes dentro de um bloco de dados alguns extrapolam o valor médio dos demais, e se por exemplo, o valor médio pode ser codificado com 5 bits, porque todo o bloco deve ser transmitido com 8 bits por causa de 10% dos dados?
O código de Huffman é a solução ideal para este tipo de problema. A idéia é utilizar uma Tabela de Conversão para converter os dados de entrada, que possuem numero fixo de bits em outros, de largura variável, onde dados de maior ocorrência possuem menos bits e dados de menor ocorrência possuem mais bits para sua representação. Desta forma, consegue-se, em média, transmitir-se menos bits. Tomemos o exemplo de uma distribuição de diferenças representadas por 3 bits (de -3 à +3) cuja codificação de Huffman é apresentada na Tabela 2, onde a ocorrência básica é dos valores -1, 0 e +1 e os demais valores (-3,-2,+2,+3) raramente ocorram. Fica claro que o tamanho do bloco enviado será menor, visto que o valor “0”, de maior ocorrência, é codificado com apenas um bit.
Tabela 2
Sample Value PCM Code Huffman Code
-3 101 1100
-2 110 1101
-1 111 100
0 000 0
+1 001 101
+2 010 1110
+3 011 1111
Para o áudio, cuja distribuição estatística de amplitude tende para a Laplaciana, a utilização da codificação de Huffman reduz em média 1.5 bits por amostra. Imaginemos que o Encoder trabalhe, por exemplo, com 8 bits para representar as diferenças e possua um conjunto de tabelas de codificação Huffman possíveis. Ao analisar o bloco de diferenças, escolhe a melhor tabela e envia, no header do bloco apenas a informação da tabela utilizada na codificação do bloco. O Decoder, que possui as mesmas tabelas, reconstrói o bloco de diferenças a partir da tabela selecionada passando ao preditor inverso os dados com largura constante (neste caso, 8 bits).
O sistema completo
O sistema completo proposto seria então composto de diversos blocos, onde o Decoder possuiria as funções inversas realizadas pelo Encoder. Seriam estes:
* Bloco de avaliação de redundâncias de bits (o qual reduz o comprimento médio da palavra por supressão de bits de sinal - os quais caracterizam o valor médio do bloco. Ver primeiro exemplo).
* Filtro de Predição & Tabela de filtros e/ou coeficientes de filtro
* Huffman Encoder (Decoder) & Tabelas de codificação
É óbvio que as atuais filosofias e algoritmos de Packing não chegam perto, em termos de redução de dados, das tecnologias “Lossy”, principalmente aquelas que fazem uso da psicoacústica e de mascaramento, porém é o caminho natural para o áudio de alta qualidade, que exige cada vez mais definição, pureza, detalhamento, cristalinidade, dinâmica, …
III - Modelos & Implementações
Como modelos e implementações das mencionadas, podemos citar alguns exemplos:
III.1 - apt-X100 e AptQ
III.2 - Dolby AC-2/AC-3
III.3 - PASC
III.4 - ATRAC
III.5 - MUSICAM
III.6 - ASPEC
III.7 - ISO/MPEG Layer I
III.8 - ISO/MPEG Layer II
III.9 - ISO/MPEG Layer III
III.1 - APT-X100
O Codec da Áudio Processing Technology, o APTX100, um DSP dedicado que pode ser configurado de diversas formas, usa Adaptive Predictive e Sub Band Coding (4 bandas) para obter uma taxa de compressão de 4:1. As bandas são obtidas de Quadrature Mirrors Filters, sendo implementado em cada uma um Preditor Adaptativo Continuo, eliminando a necessidade do processamento por blocos. O bloco de saída é composto de 2048 bits, começando por um pattern de sincronismo. Como o Codec processa no domínio do tempo de forma preditiva adaptativa, não é necessário um modelo preciso de mascaramento ou grande numero de bandas, resultando em um delay de processamento baixo e constante (menor que 4 mS), extremamente eficiente em aplicações em tempo real. Outra vantagem deste Codec é a grande imunidade a bit errors.
III.2 - DOLBY AC-2
O Algoritmo de Compressão AC-2 da Dolby caracteriza uma família de Transform Coders baseados em TDAC (Time Domain Aliasing Cancellation) e permite diversas configurações de delay e bit rate. O sinal de áudio passa através de uma transformada TDAC com window 50% overlapped critically sampled que faz uso de transformadas modificadas de seno e cosseno. Os coeficientes são agrupados em sub bandas aproximadamente equivalentes as bandas críticas. Os coeficientes em cada banda são normalizados e expressos na notação Floating Point Block com um único expoente. Estes expoentes nada mais são que a representação logarítmica da envoltória espectral do sinal e são utilizados pelo modelo perceptivo de mascaramento que requantiza as mantissas dos coeficientes.
III.3 - PASC
Precision Adaptive Sub-Band Coding (PASC) foi desenvolvido pela PHILIPS para ser utilizado no digital compact cassette (DCC). O PASC usa 32 Sub Bandas iguais geradas por um Polyphase QMF de 512 taps, sendo cada banda codificada via Floating Point Block. A energia do sinal em cada banda é calculada e comparada com o threshold absoluto do modelo auditivo e é então realizado o primeiro mascaramento. A quantidade de energia nas bandas acima do nível absoluto de mascaramento é computada de forma a determinar o mascaramento entre bandas, assim determinando o comprimento das mantissas em cada bloco.
III.4 - ATRAC
O ATRAC (Adaptive Transform Acoustic Coder) foi desenvolvido pela SONY e é utilizado no MiniDisk. O ATRAC usa uma combinação de Sub Band Coding com MDCT (Modified Discrete Cosine Transform) Coding. O sinal passa por um QMF que divide o espectro em duas bandas. A banda inferior passa por outro QMF que a divide em duas outras, enquanto que a banda superior passa por um delay para compensar o processamento do segundo QMF. Cada banda é formatada em blocos de amostras que são enviados a MDCT’s. O resultado das três MDCT’s são agrupados em 52 nódulos de frequência, que possuem largura de banda variável, aproximando as bandas críticas do sistema auditivo. A requantização é feita com base no modelo de mascaramento. Os blocos de amostras nos quais as bandas são formatadas, são adaptativos de forma a evitar noise pré-echo, variando de 1,45 mS (no caso de grandes transientes) até 11,6mS (quando a forma de onda do sinal é caracteristicamente estacionária). O tamanho do bloco é selecionado de forma independente em cada uma das três bandas. Este algoritmo comprime no MiniDisc um sinal de 16 bits PCM 44.1kHz na taxa de 5:1.
(Para maiores detalhes sobre o MiniDisc ou ATRAC ver artigo na revista SET n.42 Set/Out 98 de Hugo de Souza Melo)
III.5 - MUSICAM
O algoritmo MUSICAM (Masking Pattern Adapted Universal Sub-Band Integrated Coding and Mutiplex) nasceu do Projeto Eureka 147 DAB (Digital Áudio Broadcasting), fruto da associação da CCETT (França), IRT (Alemanha) e da Philips (Holanda). Este algoritmo é um misto de Sub Band Coding e Transform Coding. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. As amostras de cada banda são agrupadas em blocos de tamanho constante e igual a 12 amostras. Este tamanho de bloco foi baseado no fenômeno de pre-masking. Cada sub-band block é comprimido de acordo com o valor de pico do bloco e o mesmo possui um fator de escala de 6 bits (expoente). O modelo perceptual de mascaramento é implementado por uma FFT (Fast Fourier Transform) de 1024 pontos, resultando numa analise do espectro do sinal 8 vezes melhor que a largura de cada sub-banda. As mantissas de cada bloco são requantizadas de acordo com este modelo. Este algoritmo permite taxas de compressão entre 4:1 e 12:1, com delay de processamento de 8mS a mais de 30mS.
III.6 - ASPEC
O Algoritmo ASPEC (Adaptive Spectral Perceptual Entropy Coding) foi desenvolvido em conjunto pelo AT&T Bell Laboratories, Thomson Consumer Electronics, Fraunhofer Society e CNET visando a Norma estabelecida pelo ISO/IEC JTC1/SC2/WG11 experts group (MPEG/Áudio). Este algoritmo de compressão é baseado em Transform Coding. Uma MDCT em amostragem crítica (decimada de 2) com janelas adaptativas sobrepostas (1024 & 256 amostras respectivamente) é utilizada, sendo matematicamente equivalente a um banco de filtros de 512 bandas. Para bit rates elevados (96 e 128 kbits/s) um modelo psico-acústico simplificado é utilizado, porém para taxas de compressão maiores (bit rate de 64 kbits/s) um sofisticado modelo é implementado através de uma FFT de 1024 pontos. A requantização (compressão) dos coeficientes é implementada por um quantizador não linear, adaptativo, com base na analise temporal do erro de requantização segundo o modelo de mascaramento.
III.7 - ISO/MPEG Layer I
A ISO (International Organization for Standardization) e a IEC (International Electrotechnical Commission) em 1988 criaram o ISO/IEC/MPEG (Moving Pictures Experts Group) para o estudo, definição e estandardização dos esquemas de codificação para os futuros produtos para vídeo digital. No que se refere ao áudio, foi criado um grupo específico, o MPEG/Áudio.
O algoritmo standard ISO/MPEG Layer I é uma versão simplificada do MUSICAM. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. As amostras de cada banda são agrupadas em blocos de tamanho constante e igual a 12 amostras. Este tamanho de bloco foi baseado no fenômeno de pre-masking. Cada sub-band block é comprimido de acordo com o valor de pico do bloco e o mesmo possui um fator de escala de 6 bits (expoente). O modelo perceptual de mascaramento é obtido da analise espectral de cada banda.
III.8 - ISO/MPEG Layer II
Esta norma é idêntica a MUSICAM.
III.9 - ISO/MPEG Layer III
Este é o layer mais complexo da norma ISO. Ele só deve ser utilizado quando for necessário uma alta qualidade em taxas de transmissão muito baixas. É um algoritmo baseado em Transform Coding, misto do MUSICAM e ASPEC. Um Polyphase Quadrature Mirror Filter Network divide o espectro de áudio em 32 bandas de mesma largura. Cada uma das bandas são processadas por um MDCT de 12 bandas de forma a obter 384 coeficientes. Dois tamanhos de janela são utilizados para mascarar o pré-echo gerado por transientes e o chaveamento destas janelas é controlado pelo modelo psico-acústico. Foi determinado que o pré-echo ocorre quando a entropia do áudio cresce acima do valor médio. Um modelo perceptual de alta precisão é implementado fazendo uso da grande resolução de frequência disponível. A requantização é não uniforme.